Lewko's blog

The Eberhard-Green-Manners Sum-free Subset Theorem, and `What is Sum-free(13)?’

Posted in math.CO, Open Problem by Mark Lewko on February 19, 2013

The first research level math problem I seriously worked on (without much success) was the sum-free subset problem. A sum-free set (in an additive group) is a set that contains no solution to the equation x+y=z.  The sum-free subset problem concerns the following theorem of Erdős, which is one of the early applications of the probabilistic method.

Theorem: (Erdős, 1965) Let A be a finite set of natural numbers. There exists a sum-free subset S \subseteq A such that |S| \geq \frac{1}{3}|A| + \frac{1}{3}.

The natural problem here is to determine how much one can improve on this result. Given the simplicity of the proof, it seems that one should be able to better. However, the best result to date is \frac{|A|}{3}+ \frac{2}{3} (for |A|>2) due to Bourgain (1995) using Fourier analysis. It seems likely that there is a function f(n) \rightarrow \infty such that one may take |S| \geq \frac{|A|}{3}+ f(|A|) in the above theorem, however proving this seems to be quite challenging.  On the other hand proving a good upper bound also was a longstanding open problem, namely deciding if the constant \frac{1}{3} could be replaced by a larger constant. This problem, in fact, has received a fair amount of attention over the years. In his 1965 paper Erdos states that Hinton proved that the constant is at most \frac{7}{15} \approx .467 and that Klarner improved this to \frac{3}{7}. In 1990 Alon and Kleitman improved this further to \frac{12}{29} \approx 0.414, and Malouf in her thesis (as well as Furedi) improved this further to \frac{2}{5} = .4. A couple years ago I improved this to \frac{11}{28} \approx .393 (I recently learned that Erdős claimed the same bound without a proof in a handwritten letter from 1992). More recently, Alon improved this to \frac{11}{28} - 10^{-50000} (according to Eberhard, Green and Manners, Alon’s paper doesn’t appear to be electronically available. UPDATE: Alon’s paper can be found here). All of these results (with the exception of Alon’s) proceed simply be constructing a set and proving its largest sum-free subset is at most a certain size (then an elementary argument can be used to construct arbitrarily large sets with the same constant: see this blog post of Eberhard). On the other hand, it is obvious from the statement of the theorem above that one can’t have a set whose largest sum-free subset is exactly \frac{|A|}{3}, thus a simple proof by example is hopeless. The futile industry of constructing examples aside,  I spent a lot of effort thinking about this problem and never got very far.

About a month ago Sean Eberhard, Ben Green and Freddie Manners solved this problem, showing that \frac{1}{3} is indeed the optimal constant!  I don’t yet fully understand their proof, and will refer the reader to their introduction for a summary of their ideas.  However, having learned the problem’s difficulty firsthand, I am very pleased to see it solved.

In the wake of this breakthrough on the upper bound problem, I thought I’d take this opportunity to highlight a toy case of the lower bound problem.

Definition: For a natural number n define the sum-free subset number Sum-free(n) to be the largest number such that every set of n natural numbers is guaranteed to contain a sum-free subset of size at least Sum-free(n).

Thus by Bourgain’s theorem we have that Sum-free(n) \geq \frac{n+2}{3} (and the Eberhard-Green-Manners theorem states Sum-free(n)=\frac{n}{3}+o(1)). It turns out that Bourgain’s result is sharp for sets of size 12 and smaller. However, Bourgain’s theorem only tells us that a set of size 13 must contain a sum-free subset of size 5 while it seems likely (from computer calculations) that every set of size 13 must in fact contain a sum-free subset of size 6. Indeed, I’ll even

Conjecture: Sum-free(13)=6.

While the asymptotic lower bound problem (showing that there f(|A|) \rightarrow \infty) seems very hard and is connected with subtle questions in harmonic analysis (such as the now solved Littewood conjecture on exponential sums), this problem is probably amenable to elementary combinatorics (although, it certainly does not seem easy!). Below is a chart showing what I know about the first 15 sum-free subset numbers.

 

n Bourgain’s lower bound
on Sum-free(n)		 Best known upper
bound on Sum-free(n)		 Upper bound set example
1 1 1 \{1\}
2 1 1 \{1,2\}
3 2 2 \{1,2,3\}
4 3 3 \{1,2,3,4\}
5 3 3 \{1,2,3,4,5\}
6 3 3 \{1,2,3,4,5,6\}
7 3 3 \{1,2,3,4,5,6,8\}
8 4 4 \{1,2,3,4,5,6,7,9\}
9 4 4 \{1,2,3,4,5,6,7,8,10\}
10 4 4 \{1,2,3,4,5,6,8,9,10,18\}
11 5 5 \{1,2,3,4,6,10,20,70,140,210,420\}
12 5 5 \{1,2,3,4,5,6,7,8,9,10,14,18\}
13 5 6 \{1,2,3,4,6,10,20,35,70,105,140,210,420\}
14 6 6 \{1,2,3,4,5,6,7,10,12,14,30,35,60,70\}
15 6 7 \{1,2,3,4,6,10,20,30,35,60,70,105,140,210,420\}

7 comments

7 Responses

Subscribe to comments with RSS.

  1. Sean Eberhard said, on October 24, 2013 at 10:38 am

    Dear Mark,

    It’s worth pointing out that computing values of sum-free(.) is a finite task: for every n there is some N (where I think N ~ 4^n suffices) such that every set of n elements is Freiman-isomorphic to a subset of {1,..,N}, so it suffices to check all n-element subsets of {-N,…,N}. Still, computing sum-free(13) with this approach per se is probably impractical.

    Of course, proving an asymptotic lower bound would be much more interesting.

    Reply
    • Mark Lewko said, on October 24, 2013 at 1:58 pm

      Hi Sean,

      Thanks for the comments!

      Before we knew much combinatorics, Allison and I proved that the problem was finitary using linear programming. Of course, we later learned this is well-known in the context from Freiman isomorphism theory, as you point out.

      This does lead to other interesting question that I never did figure out. For instance, how may Freiman-isomorphic classes are there of size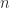 n? This should be considerably smaller than 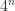4^n choose 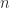n. Also, it seems that the isomorphism classes that have sets with elements near 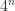4^n won’t have very many sum relations (which makes them not very interesting in the context of the problem). Perhaps there is hope that one can get the computation down to something reasonable for small cases, such as 13.

      It’s also interesting to consider this in the context of approaching the asymptotic lower bound problem. Given Bourgain’s work, it is natural to proceed by attempting to classifying the near extermizers to the Littlewood conjecture. That is, classify the sets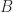 B such that 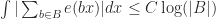\int | \sum_{b\in B} e(bx) | dx \leq C \log(|B|) . However, as far as I can see, once one reduces to this problem, one looses the finitary property described above. Similarly, the Littlewood problem is translation invariant, while the sum-free subset problem isn’t. So it seems one looses quite a bit in this reduction.

      Reply
      • Sean Eberhard said, on October 24, 2013 at 3:12 pm

        As it happens, I was also just wondering how many Freiman-isomorphism classes of size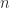 n there are. I don’t know. I agree it’s probably not too large, but one would also need a way of iterating through them efficiently. Maybe it would be more practical to try to prove directly that sets that don’t have Freiman models with reasonably small diameter automatically have large sum-free subsets: certainly this is true of {0} \union powers of two, the usual example of a set with large diameter.

        Using Bourgain’s work, it would be enough to prove that sets with small L^1-hat norm have dense Freiman models, but this seems difficult.

      • Mark Lewko said, on October 24, 2013 at 9:25 pm

        Sean, In your last comment, by dense model, do you mean that the density in an arithmetic progression is asymptotically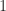 1, or just positive? I believe the first, but have tried to prove the second without success. I saw that Ben Green claims to have a proof of something along these lines in his talk at http://kva.screen9.tv/#gipkF4pTSbAL16tJjJzj8Q, but it is rather unclear what the claim is exactly.

    • Seva Lev said, on December 3, 2013 at 11:03 am

      Dear Sean,

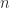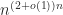      This is actually a reply to your post *below* — which was itself intended as a reply and for this reason does not provide a “reply” button. Anyway, the total number of Freiman-isomorphism classes of size n is n^{(2+o(1))n}, as shown in our join paper with Konyagin “Combinatorics and linear algebra of Freiman isomorphism”; it is available at http://math.haifa.ac.il/~seva/Papers/colifr.dvi

      Reply
      • Mark Lewko said, on December 3, 2013 at 2:24 pm

        Seva, thanks for the reference! Using the argument from your paper with Konyagin, it seems that it should be computationally feasible to check the case of Sum-free(13).

        It would be particularly exciting if one could find a way to use an improved lower bound for small values of Sum-free(n) as part of an induction to get an improvement for larger sets as well.

  2. Sean Eberhard said, on October 25, 2013 at 7:19 am

    I just mean positive. My source is some published notes of Ben’s. I’m not sure how much of it he’d like me explaining on the internet, but in any case I guess the main difficulty is proving any sort of structure for sets with small L^1-hat norm.

    Reply

Leave a comment